벡터의 내적(C++)

매번 엔진함수로만 내적계산을하다 이번에 내적을 C++로 구하는일이 생겨서 보니 모르겠어서

개인적인 공부겸  벡터의 내적계산을 C++로 하는방법을 간단하게 정리해봤다.

 

이전에 정리한 내적공식은 다음과같다.

 

AㆍB = |A| |B| cosθ

 

A내적B = 벡터A크기 * 벡터B크기 * cosθ

cosθ = A내적B / A크기 / B크기

θ = Arccos(A내적B / A크기 / B크기)

 

벡터 내적을 단순 수학으로 어떻게하는질몰랐었는데 찾아보니 그냥 단순 좌표곱의 합이였다..

위 수식을 C++로 표현하면 다음과같다.

 

const double PI = 3.1415926;

int main() 
{
	double x = 1;
	double y = 2;

	double x2 = -1;
	double y2 = 2;

	cout << x * x2 + y * y2 << endl;

	cout << (x * x2 + y * y2) / sqrt(x * x + y * y) / sqrt(x2 * x2 + y2 * y2) << endl;

	double angle = acos((x * x2 + y * y2) / sqrt(x * x + y * y) / sqrt(x2 * x2 + y2 * y2)) * 180 / PI;

	cout << angle << endl;

	cout << cos(angle * (PI/180));

}

 

180 / PI는 라디안값을 각도로 변환시키기위한 과정이다.

역으로 각도를 라디안으로 변환시킬때는 PI / 180을 곱하면된다.

 

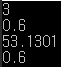
결과가 이렇게나온다. 한가지 주의할점이 Cos(90도)의경우 원래 값이 0이나와야되지만

const double PI = 3.1415926;

int main() 
{
	double x = 2;
	double y = 2;

	double x2 = -2;
	double y2 = 2;

	cout << x * x2 + y * y2 << endl;

	cout << (x * x2 + y * y2) / sqrt(x * x + y * y) / sqrt(x2 * x2 + y2 * y2) << endl;

	double angle = acos((x * x2 + y * y2) / sqrt(x * x + y * y) / sqrt(x2 * x2 + y2 * y2)) * 180 / PI;

	cout << angle << endl;

	cout << cos(90 * (PI/180));

}

 

코드를 다음처럼해서 90도각도가 나오게 두좌표를 수정하고 테스트해보면 

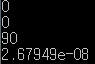
결과가 이렇게나온다. 

0.000000267949 정도의 숫자라고하는데 조건문을사용할때 주의가 필요할듯싶다.